Hoy día en las aulas de clase, en las asignaturas del pregrado en Economía, se empieza enseñando la Teoría del consumidor, tema de un gran campo de la economía, que es la Microeconomía. Sin embargo, siempre se enseña la teoría sin poder ver su aplicación pragmática en la vida real. Por tanto, este artículo tiene como objetivo introducir a los lectores en temas de economía aplicando, especificamente estas teorías, en un lenguaje de programación como lo es Python.
Para este artículo haremos uso de Python 3, además es necesario instalar las librerías numpy, matplotlib y scipy como se describe a continuación:
1
2
3
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import minimize
Se llama la librería numpy ya que en código posterior haremos uso de métodos que nos simplificarán la expresión de funciones en Python. Así mismo se llama la librería matplotlib.pyplot con el fin de graficar las funciones que posteriormente se mencionarán relacionadas a la utilidad de ciertos bienes. Finalmente se usará scipy.optimize con el fin de realizar la optimización de la función de utilidad como ejemplo a través del método SLSQP.
Teoría del consumidor
La teoría del consumidor es aquella rama de la microeconomía encargada de analizar el comportamiento de los agentes económicos, específicamente de cómo asignan su renta en la compra de bienes con el fin de obtener el mayor bienestar posible.
Se continuará teniendo en cuenta a la teoría neoclásica del consumidor basada en las preferencias del agente económico y su respectiva restricción presupuestal.
Función de utilidad
Es aquella función que asigna cierto nivel de utilidad (o bienestar) a una cesta de bienes de mercado, dado las preferencias del agente económico frente a estos bienes. Ejemplos de funciones de utilidad:
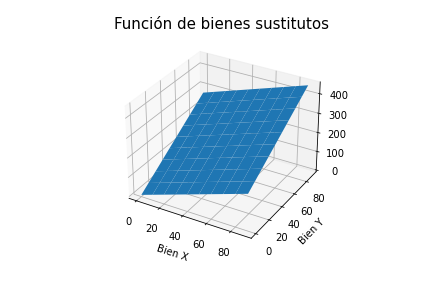
- Función de bienes sustitutos:
En este caso, dos bienes (X, Y) son sustitutos perfectos si el consumidor está dispuesto a sustituir un bien por otro a una tasa constante.
1
2
3
4
5
6
7
8
9
10
11
12
13
x=y=np.arange(0.0, 100, 10)
X, Y=np.meshgrid(x,y)
def funcion_objetivo(x,y):
a=2
b=3
return(x*(a)+y*(b))
fig=plt.figure()
ax=fig.gca(projection='3d')
ax.plot_surface(X,Y, funcion_objetivo(X,Y))
ax.set_ylabel("Bien Y")
ax.set_xlabel("Bien X")
ax.set_title("Función de bienes sustitutos", fontsize=15)
plt.savefig('sustitutos.png')
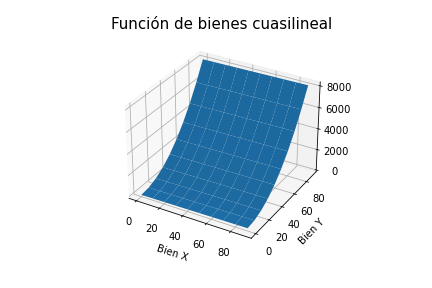
- Función Cuasilineal:
Para este caso, el bien X es lineal; por tanto el bien Y depende exclusivamente de la relación de precios (p1/p2) y no de la renta del consumidor, como si es el caso de X.
1
2
3
4
5
6
7
8
9
10
x=y=np.arange(0.0, 100, 10)
X, Y=np.meshgrid(x,y)
Z=X+Y**2
fig=plt.figure()
ax=fig.gca(projection='3d')
ax.plot_surface(X,Y, Z)
ax.set_ylabel("Bien Y")
ax.set_xlabel("Bien X")
ax.set_title("Función de bienes cuasilineal", fontsize=15)
plt.savefig('cuasilineal.png')
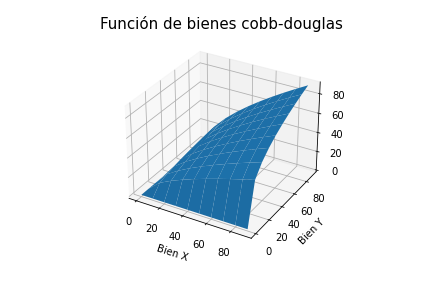
- Función Cobb-Douglas:
Una característica de esta función es que la suma de los exponentes debe dar uno para que la solución de la optimización se un óptimo global.
1
2
3
4
5
6
7
8
9
10
11
12
13
x=y=np.arange(0.0, 100, 10)
X, Y=np.meshgrid(x,y)
def funcion_objetivo(x,y):
alfa=2/3
beta=1/3
return(x**(alfa)*y**(beta))
fig=plt.figure()
ax=fig.gca(projection='3d')
ax.plot_surface(X,Y, funcion_objetivo(X,Y))
ax.set_ylabel("Bien Y")
ax.set_xlabel("Bien X")
ax.set_title("Función de bienes cobb-douglas", fontsize=15)
plt.savefig('cobb.png')
Elección del consumidor:
El consumidor debe elegir la cesta de bienes que maximiza su bienestar, en este caso utilidad, sujeto a la restricción presupuestal dado los precios de los bienes en el mercado y sus ingresos. Dado lo anterior, el consumidor debe gastar su renta en no mas de:
\[\begin{aligned} p_xX +p_yY \end{aligned}\]Este es el caso para dos bienes.
Por tanto, el conjunto presupuestal en el cual el consumidor debe elegir la canasta es:
\(\begin{aligned} [(X,Y)| p_xX+p_yY\leq W] \end{aligned}\) Donde w es wage.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
x=np.arange(0.0, 1000, 10)
w=1500
p=[2,8]
y=w/p[1]-(p[0]*x/p[1])
plt.plot(x,y)
#plt.plot(sol.x)
plt.ylim([0,250])
plt.xlim([0,900])
plt.xlabel("Bien X")
plt.ylabel("Bien Y")
plt.title("Restriccion presupuestal")
plt.text(250, 80, "- p1 / p2")
plt.fill_between(x, y,1, color="grey")
plt.show()
plt.savefig('restriccion.png')

Además, dado el supuesto de no saciabilidad de las preferencias del agentes económicos, el conjunto presupuestal se vuelve en una recta presupuesta también contiene las cestas de bienes donde el costo de las mismas es igual a la renta. $ p_xX+p_yY=W$ Así que el problema de elección del consumidor queda resumido en la siguiente maximización:
\[\begin{aligned} Max U(X,Y)\\ p_xX+p_yY=W \\ X, Y\geq 0 \end{aligned}\]A continuación un ejemplo mostraremos la maximización de una función Cobb-Dougglas con su respectivo código en Pyhton.
\[\begin{aligned} Max U(X,Y)=x^{2/3}y^{1/3}\\ p_xX+p_yY=1500\\ X, Y\geq 0 \end{aligned}\]
Dado que la mayoría de los programas para optimización realizan solamente la minimización de las funciones (como es el caso de Python), es necesario convertir la función objetivo en una función negativa como se describe a continuación, para así obtener el resultado de la maximización.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
def restriccion_1(x):
w=1500
p=[2,8]
return -w+p[0]*x[0]+p[1]*x[1]
def objetivo(X):
x,y=X
alpha=2/3
beta=1/3
return -(x**(alpha)*y**(beta))
b=(0,None)
bnds=(b,b)
restriccion=[{'type':'eq', 'fun':restriccion_1}]
sol=minimize(objetivo, (0,0), method="SLSQP", constraints=restriccion, bounds=bnds)
optimo=sol.x
La solución analítica de este problema es (X = 500 y Y = 62,5). Sin embargo, Python nos arroja una solución por métodos numéricos que es (X = 499,9 y Y = 62,5) la cual esté muy cerca a la solución analítica. A continuación la gráfica con la solución numérica.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
x=y=np.arange(0.0, 1000,10)
X,Y=np.meshgrid(x,y)
def func_(f,X,Y):
s=np.shape(X)
return f(np.vstack([X.ravel(),Y.ravel()])).reshape(*s)
def objetivo(X):
x,y=X
alpha=2/3
beta=1/3
return (x**(alpha)*y**(beta))
w=1500
p=[2,8]
fig, ax=plt.subplots(figsize=(8,6))
c=ax.contour(X,Y, func_(objetivo,X,Y), 40)
ax.plot(optimo[0], optimo[1], "b*")
ax.plot(x, w/p[1]-(p[0]*x/p[1]))
ax.fill_between(x, w/p[1]-(p[0]*x/p[1]),1, color='grey')
ax.set_ylim(0, 300)
ax.text(optimo[0], optimo[1], "%s, %s"%(optimo[0], optimo[1]))
ax.set_ylabel("Bien Y")
ax.set_xlabel("Bien X")
ax.set_title("Optimo", fontsize=15)
plt.savefig("optimo.png")
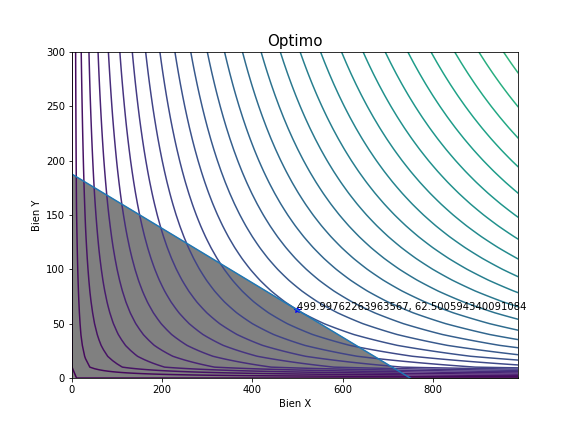
Como se puede observar, la teoría económica enseñada día a día en los claustros universitarios se pueden enseñar también con la nueva corriente de enseñanza en programación computacional. Así, este artículo hace la invitación al lector a incurrir más en el mundo de la programación, la cual ayudará a la formación de profesionales más integrales para el mercado laboral.
Referencias:
- Guerrera, J., Sánchez, A. & Zambrano, A. (2006). Notas de Microeconomía I.
- Carvajal, A., Riascos, A. (2012). Introducción a la Teoría Micreconómica.
- http://www.eco.uc3m.es/docencia/microeconomia/Transparencias/M1.pdf.
- http://allman.rhon.itam.mx/~aburto/eco%203/Preferencias_y_utilidad_del_consumidor_2010_a.pdf.
