El solicitar préstamos es una de las operaciones bancarias más usadas por el ciudadano de a pie con el fin de tener dinero para invertir o gastar en necesidades, dinero que antes no tenía a disposición. Sin embargo, estos préstamos o crédito no son gratis, tienen un precio y este precio es la tasa de interés. Cada entidad bancaria en cada país manaje su propia tasa de interés según el producto que desean solicitar, ejemplo de esto son créditos para consumo, hipotecarios, vivienda, entre otros.
Previo a solicitar estos préstamos, es necesario conocer las diferentes modalidades que existen para así no incurrir en incumplimientos de pago que conlleven a reportes negativos en los buros como Datacrédito, para el caso colombiano.
En primer medida, el valor del préstamo estará muy afectado por el precio en este caso, la tasa de interés, al igual que la modalidad de pago que se vaya a usar. Por ejemplo, no es lo mismo pactar realizar un pago mensual de la misma cantidad, a pactar una cuota mensual variable que dependa de los intereses a pagar; así mismo depende si se va a realizar el pago de una cuota inicial o no.
En esta ocasión, mostraremos cómo realizar un simulador de créditos con cuotas fijas a través de python, lo cual puede ser de mucha ayuda a la hora de pedir un préstamo a alguna entidad bancaria.
Generación del simulador
Primero se deben instalar y llamar las librerías necesarias. La librería principal que usaremos es numpy_financial la cual nos ayudará a calcular la cuota a pagar en cada mes; sin embargo, también se puede usar para calcular las tasas de interés y saldos.
1
2
3
4
5
6
7
! pip install numpy_financial
import numpy as np
import pandas as pd
import numpy_financial as npf
import warnings
warnings.filterwarnings('ignore')
Luego de esto, se debe definir los parámetros del simulador los cuales serían la tasa de interés mes vencido, el monto a financiar, el plazo de meses a pagar (la periodicidad de este simulador es mensual) y por último la cuota inicial a pagar, si se necesita.
1
2
3
4
tasa=0.0109
monto_financiar=500000
plazo=18
cuota_inicial=0
Para este caso, asumimos una tasa de interés del 1.09%MV, con un valor a financiar $500.000 pesos colombianos a 18 meses en donde la cuota inicial es de 0, es decir que no todo el pago abona a capital, sino que también paga los intereses. Luego, generamos una función que relacione el cálculo de cuotas y genere una tabla de amortización del crédito para cada mes de referencia. La función pide ingresar el número de cuotas iniciales a pagar, para este caso es 0 (la función solamente procesara cuando son créditos con una cuota inicial o sin cuota).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
def cuota_fija(tasa,monto_financiar, plazo, cuota_inicial ):
base_liquidador=pd.DataFrame([])
cuota=npf.pmt(tasa, plazo,-monto_financiar, 0)
cuotas_iniciales=int(input("Ingrese el valor: "))
if cuotas_iniciales==1:
base_liquidador=pd.DataFrame([])
base_liquidador['Mes_cuota']=["Mes_%s"%(i+1) for i in range(plazo+1)]
base_liquidador['Saldo']=0
base_liquidador['Intereses']=0
base_liquidador['Saldo'][0]=monto_financiar
base_liquidador['Saldo'][1]=monto_financiar-cuota_inicial
base_liquidador['pago_mes']=int(cuota)
base_liquidador['pago_mes'][0]=cuota_inicial
base_liquidador['amortización']=0
base_liquidador['amortización'][0]=cuota_inicial
base_liquidador['tasa_interes']=tasa
base_liquidador['Saldo_final']=0
for i in range(0, len(base_liquidador)):
base_liquidador['Intereses'][i+1]=(base_liquidador['Saldo'][i]*base_liquidador['tasa_interes'][i])
base_liquidador['amortización'][i]=np.where(base_liquidador['Saldo'][i]>base_liquidador['Intereses'][i],(base_liquidador['pago_mes'][i]-base_liquidador['Intereses'][i]),base_liquidador['Saldo'][i] )
base_liquidador['Saldo'][i+1]=base_liquidador['Saldo'][i]-base_liquidador['amortización'][i]
base_liquidador['pago_mes'][i]=np.where(base_liquidador['Saldo'][i]>base_liquidador['amortización'][i], base_liquidador['pago_mes'][i], base_liquidador['Saldo'][i])
base_liquidador['Saldo_final'][i]=base_liquidador['Saldo'][i]-base_liquidador['amortización'][i]
elif cuotas_iniciales==0:
base_liquidador=pd.DataFrame([])
base_liquidador['Mes_cuota']=["Mes_%s"%(i+1) for i in range(plazo)]
base_liquidador['Saldo']=0
base_liquidador['Saldo'][0]=monto_financiar
base_liquidador['Intereses']=0
base_liquidador['pago_mes']=int(cuota)
base_liquidador['amortización']=0
base_liquidador['tasa_interes']=tasa
base_liquidador['Saldo_final']=0
for i in range(0, len(base_liquidador)):
base_liquidador['Intereses'][i]=(base_liquidador['Saldo'][i]*base_liquidador['tasa_interes'][i])
base_liquidador['amortización'][i]=np.where(base_liquidador['Saldo'][i]>base_liquidador['Intereses'][i],(base_liquidador['pago_mes'][i]-base_liquidador['Intereses'][i]),base_liquidador['Saldo'][i] )
base_liquidador['Saldo'][i+1]=base_liquidador['Saldo'][i]-base_liquidador['amortización'][i]
base_liquidador['Saldo_final'][i]=base_liquidador['Saldo'][i]-base_liquidador['amortización'][i]
else:
print("Oops! Este es un valor incorrecto. Pruebe de nuevo...")
return base_liquidador
luego, se debe correr la función con los valores generador para este simulador.
1
2
df=cuota_fija(tasa,monto_financiar, plazo, cuota_inicial )
print(df)
Gráficas del amortizador
La siguiente tabla refleja el comportamiento del amortizado a lo largo de los 18 meses.
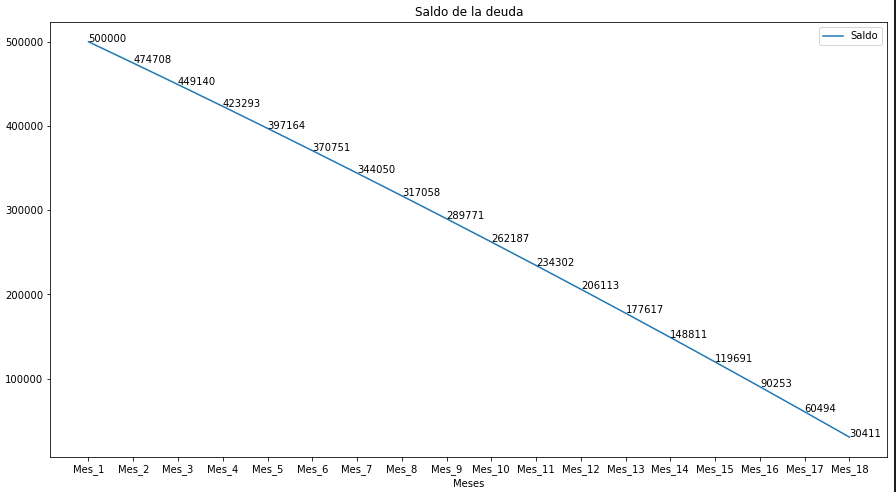
Con el siguiente código realizaremos la gráfica del saldo capital del crédito.
1
2
3
4
5
6
7
8
9
10
import matplotlib.pyplot as plt
plt.figure(figsize=(15,8))
plt.plot(df.Mes_cuota,df.Saldo,label='Saldo')
plt.xlabel('Meses')
plt.gcf().axes[0].yaxis.get_major_formatter().set_scientific(False)
plt.title('Saldo de la deuda')
for a,b in zip(df.Mes_cuota,df.Saldo):
plt.text(a, b, str(b))
plt.legend()
plt.show()
La siguiente gráfica refleja el comportamiento del saldo de la deuda en cada uno de los periodos del crédito.
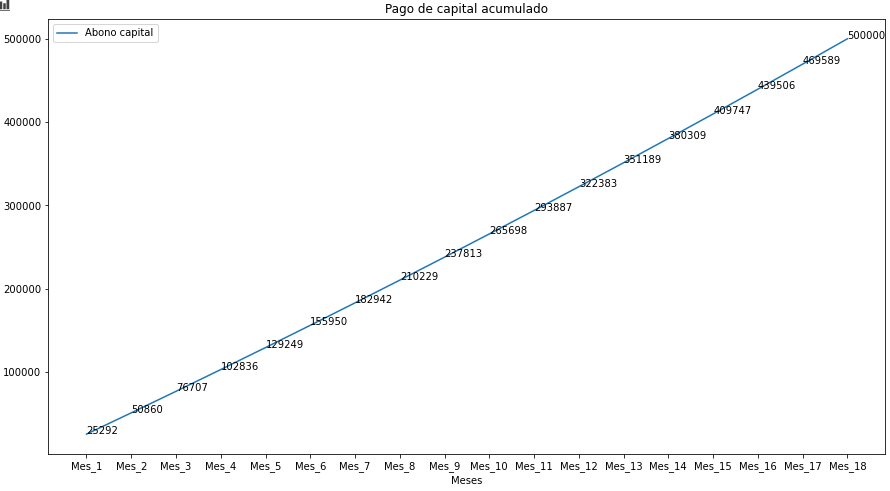
Finalmente, este código a continuación realizará la gráfica referente a la acumulación de la amortización del pago de cada periodo relacionado al crédito.
Para finalizar, es muy importante tener en cuenta ya que como dijo Albert Einstein “El interés compuesto es la octava maravilla del mundo. Quien la entiende se beneficia de ella … el que no … la paga”. Como ejercicio del lector, una buena forma de practicar eso es genera el simulador para créditos con cuota variable.